The most boring topic of the year makes a comeback! I have been struggling a bit to make robust movement along navigation mesh, but I think I finally nailed it.
Why should you care?
The basis of solid
navigation loop is good collision handling. For navigation meshes this means a way to handle movement along connected graph of convex polygons. That is, how to move from one polygon to another and how to handle the case when the desired move collides with blocking navigation mesh edge.
The method should also return the polygons it walked through during the movement. This is used to fixup the path corridor so that on next update we have valid path to follow again.
First idea: Raycast
My very first implementation of movement code used raycasts. I used similar iterative code as the good 'ol ellipsoid vs. trimesh collision detection. The problem with that solution was that the rays end up being parallel to the polygon edges when sliding or hit vertices when aiming for next corner. I ended up running into a lot of floating point accuracy errors and quite interesting special case hacks to get rid of them.
Second idea: Point in Polygon
My second attempt changed the whole idea upside down. I can calculate the sliding movement inside a convex polygon by clamping the target point to be the nearest point in the polygon. To handle the connected graph of convex polygons (like navmesh) we can check if the nearest point would lie on an edge which leads to neighbor polygon, and follow that until the goal polygon has been found.
While the basic idea is sound, here area a couple of cases where it does not produce desired result. Firstly there are some corner cases where it will miss potential move to neighbour polygon because it does not check visibility (
see my previous post). Interestingly this is not a problem when using triangles.
Second, nasty problem is that it does not handle well the case that the nearest point is at a polygon vertex. In this case either edge are equally good candidate to follow and I could not find goo heuristic which would handle all the corner cases I had in mind.
This method is a bit similar to the
jump-and-walk algorithm which is used to locate triangles in triangulation. It is known to work on triangulations which have convex boundary.
Third idea: Search
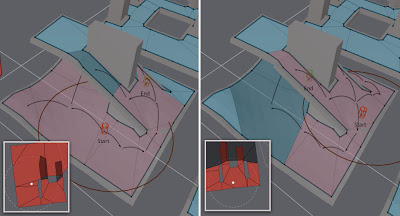
This idea extends the previous by making it breath first search instead of iterative loop. That nicely solves the problem of trying to choose good branching at each iteration, all branches are followed instead.
The search expands to all edges which touch circle containing the start and goal location (start+delta). The search is stopped when the goal polygon is found or no more polygons can be visited. In case the goal is inside a polygon, the goal location is accepted, else the nearest point to all visited blocked polygon edges is chosen.
In pseudo code it looks something like this:
// Applies constrained movement from startPos to goalPos.
// The result is stored in clampedPos.
// Returns number of visited polygons.
int Navmesh::navmeshMoveAlong(Vec3 startPos, PolyRef startRef, Vec3 goalPos,
PolyRef* visited, Vec3& clampedPos)
{
Stack stack(16); // Tiny stack
ClosedList closed(32); // Tiny closed list
Vec3 bestPos, p;
float bestDist = FLT_MAX, d;
PolyRef bestRef = UNDEF;
// Search constraint
Vec3 searchPos = (startPos+goalPos)/2;
const float searchRadius = vdist(startPos,goalPos)/2;
// Init
bestp = start;
stack.push(startRef);
closed.add(startRef,startRef); // Self ref, start maker.
while (!stack.empty())
{
// Pop front.
PolyRef cur = stack.pop();
Poly* poly = getPoly(cur);
// If target is inside the poly, stop search.
if (pointInPoly(goalPos, poly))
{
bestRef = cur;
bestPos = goalPos;
break;
}
// Follow edges or keep track of nearest point on blocking edge.
for (int i=0, j=poly->nv; i<poly->nv; j=i++)
{
const PolyRef neiRef = poly->nei[j];
const Vec3& sp = getVertex(poly->v[j]);
const Vec3& sq = getVertex(poly->v[i]);
if (neiRef == UNDEF)
{
// Blocked edge, calc distance.
p = closestPtPtSeg(goalPos, sp,sq);
d = vdist(p,goalPos);
if (d < bestd)
{
// Update nearest distance.
bestPos = p;
bestDist = d;
bestRef = cur;
}
}
else
{
// Skip already visited.
if (closed.find(neiRef)) continue;
// Store to closed with parent for trace back.
closed.add(neiRef,cur);
// Non-blocked edge, follow if within search radius.
p = closestPtPtSeg(searchPos, sp,sq);
d = vdist(p, searchPos);
if (d <= searchRadius)
stack.push(neiRef);
}
}
}
// Trace back and store visited polygons.
followVisited(bestRef,visited,closed);
// Store best movement position.
clampedPos = bestPos;
// Return number of visited polys.
return visited.size();
}
So it is a tiny special case pathfinder. The result is movement which can quite liberally move along the navmesh and if it encounters walls it will slide. The slack is necessary when you need to shortcut a little for example when very close to the next corner along the path.
The code above is meant to perform well when you do really small increments. It aims to be faster than regular pathfinder which is tuned to perform well with potentially thousands of nodes.
For such local case you may maintain the open list (stack) and closed lists using simple arrays. There are many cases in the code which may trash your cache (accessing the navmesh data), but by using small arrays for open and closed lists you can avoid some of it. Since we expect the lists to be small, we can potentially use simple linear searches which simplifies the code.
Next Step
My next task is to figure out nice way to calculate 2D local collision environment from 2.5D navmesh. This is to be used with velocity obstacles. Then I should be ready move on porting the VO code to Detour.